measuringu.com Jeff Sauro, PhD April 21, 2010
ユーザーが1つのタスクを完了するのにかける時間はどのぐらいなのか?これは本当にはわかりません。その代わり、ユーザーのサンプルから最善の推測をするしかありません。しかし、ユーザビリティテストで典型的なユーザーがタスクを完了するのにかかる時間を1つの数値にまとめるとしたら、何を報告しますか? 平均値ですか?中央値でしょうか?最頻値?他のもの?
最も一般的な値や典型的な値を表すために1つの数値を求める場合、平均値、より具体的には算術平均値を用いることが多い。サンプル(特に少量のサンプル)からの単一の推定値はほぼ確実に間違っているので、最善の推測に信頼区間を含めることが重要です。 サマリーデータは、ダッシュボードや管理者への報告書に使用されることが多いため、典型的なタスク完了時間のベストな推測値を算出する必要があります。
平均値は、ほぼ対称的なデータの中心値や最も「典型的」な値を示すのに非常に有効です。データが非常に大きな値で歪んでいる場合、平均値は上方に引っ張られます。これは、平均住宅価格や平均給与などの財務データを要約するときに起こります。非常に高価な家が1軒あったり、最高経営者がいたりすると、平均値が大きく引き上げられてしまうのです。このような場合には、中央値を使用して、中間値や最も典型的な値をより正確に把握します。
幾何平均は、サンプルサイズが25以下の場合、中央のタスク時間を最も正確に測定ていると言えます。
タスクタイムのデータが歪んでいる(正常ではない)場合
タスク時間は正に偏る傾向が強く、タスクを完了するのに時間がかかるユーザーもいます。これは、ユーザーの個人差が大きいことに起因しています。ユーザーの中には、インターフェイスに問題があったり、タスクを完了するためにコンピュータをゆっくり使う人もいます。いくつかの長いタスク時間は、平均タスク時間を引き上げ、典型的なタスク時間ではなくなります。むしろ中間値を誇張しています。例えば、タスク時間が100、101、102、103、104の場合、平均値と中央値は102になります。200のタスク時間を追加すると、平均値が118.33、中央値が102.5となり、分布が歪んでしまいます。
下の図では、正のスキュー(尾が右に向いている)を見ることができます。図1は、あるイントラネット・アプリケーションでタスクを完了した190人のユーザーのタスク時間のヒストグラムです。平均値が中央値よりも高いことに注目してください。
幾何平均と信頼区間を計算するためのエクセル計算機はこちらからダウンロードできます。
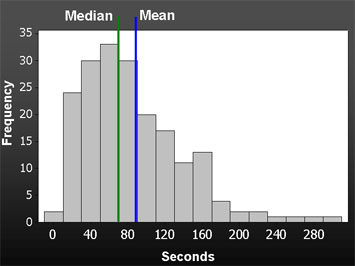
図1: 190個の完了したタスクの時間のヒストグラムで、平均に対する正のスキューの効果を示しています。このタスクの中央値は71秒で、平均値は85秒です。中央値とは、半分のユーザーがより多くの時間を要し、半分のユーザーがより少ない時間で済む点である。
サンプル数が少ない場合、中央値は実際の中間時間を10%程度過大評価する傾向があります。
なぜ中央値を報告しないのか?
では、住宅価格や給料のように、タスクタイムの中央値を報告すればいいのではないでしょうか? 大きな違いは、未知の母集団の中央値を推定するためにサンプルを使用していることです。サンプル数が多ければ、中央値はこの未知の値をよく推定できます。サンプルが少ない場合(ユーザー数が25人以下)、サンプルの中央値は、母集団の中央値の悪い推定値になる傾向があります。サンプルが小さければ小さいほど、推定値は悪くなります。
標本の中央値は母集団の中央値の推定値としては不十分
極値の影響を受けにくい中央値の強さは,エラーとバイアスという2つの問題を引き起こします.中央値は,サンプルで得られるすべての情報を利用していない.奇数番目のサンプルの場合,中央値は中心値であり,偶数番目のサンプルの場合,中央値は2つの中心値の平均である.そのため、中央値はそれぞれの平均値よりも変動しやすく、推定の誤差が大きくなります。中央値のもう一つの問題点は、実際の中央値を10%も過大評価する傾向があることです。これは、一刻を争う場合には大きな問題となります。
サンプル数が少ない場合に最適な中央値の推定方法は?
平均値を生成する方法は、文字通り何百通りもあることがわかりました。最近のCHI論文[pdf]で、Jim Lewisと私は、幾何平均、調和平均、平均を計算する前に最大時間を除外するなど、正に歪んだタスク時間を扱うための有望な方法をいくつか検討しました。
私たちがテストしなかった平均は、最頻値(最も頻度の高い値)です。タスク時間のデータは非常に多くの異なる値を取ることができるため、最頻値はタスク時間の平均には適していません。最頻値は、多くの場合、未定義 (すべてのユニークな値)、または複数の最頻値((2つの重複した値) があり、さらに悪いことに、最頻値は中心から離れた2つのタスク時間から来ています。
最良の平均値をテストするために、61の大規模サンプルのユーザビリティタスクでモンテカルロシミュレーションを行ったところ、平均して幾何平均は母集団の中央値を最もよく推定し、バイアスが最も少ないことがわかりました(中央値を過小評価する可能性も過小評価する可能性も同じです)。サンプル数が25以下の場合は、幾何平均値が勝者となります。
シミュレーション:少数のサンプルを使って中央値を推定する
このようなことがどのように行われるのかを理解していただくために,以下のシミュレーションを作成しました.
ボタンをクリックすると、図1に示した大規模なサンプルのタスクから小さなサンプルを抽出します。このタスクの中央値は71秒です。 クリックするたびに、新しいサンプルの中央値と幾何平均が計算され、時間の経過とともにバイアスとエラーの量が計算されます。 例えば、5回(36,60,81,92,105)のランダムなサンプルでは、中央値が81秒、幾何平均値が70.1秒となりました。中央値は10秒(14%)、幾何平均は0.9秒(1.3%)の誤差がありました。 データベースに登録されている61個のタスクについて、サンプルサイズが2~25の間で数千回行ったところ、幾何平均はサンプル中央値よりも誤差が13%少なく、偏りが23%少ないことがわかりました。 ボタンをクリックするたびに、190回のデータセットからランダムにタスクの時間が取得され、中央値と幾何平均値が計算され、母集団の中央値である71秒と比較されます。(計算機部分省略)